不偏分散は何故n-1で割るのか
高校数学で習う確率では、標本分散は標本(サンプル)と標本平均との差の自乗をサンプルサイズnで除し、不偏分散はn-1で除す、となんとなく習ったと思います。僕はこういうのが気になるロジカルバカだったので、解説してみようと思いました。
- 授業では省略されていた
- 不偏分散とは何か
- 標本確率変数
- 平均値(代表値)とは
- 平均偏差とは
- 標本分散とは
- 標本平均の期待値と母平均
- 賭博破戒録で学ぶ分散の基本
- 標本分散の期待値と不偏分散
- 何故学校では教えなかったのか
授業では省略されていた
学生時代、 数学の先生はどうして標本数から1引いた数で割るのかについては詳しく説明してくれなかった。
標本分散の説明が終わると、さらっと不偏分散の場合はn-1を使うという説明だったと思う。そして、授業の終わりに先生が「何か質問ある人~?」と言われたときに一度だけ質問した。(いや、3回だったかも)返答は「興味があるなら自分で解いてみろ」だった。
このとき僕は少し考えればわかることなのかと思って、時々思い出しては思考をめぐらすものの答えに辿り着くことはできなかったが、ずっとモヤモヤしていた。
この証明が結構面倒くさいということを知るのはもっと後になってからのことなのである。
そんなわけで今回はblog読者の趣味嗜好を完全に無視して記事を書いた。
勢いで。
だから、今回の記事は読み飛ばして構わない。
なんならこちらの人気記事でも読んでください。
というわけで今回はただの数式の羅列と証明の回、ただそれだけなのです。すまぬ。
不偏分散とは何か
そもそも、不偏分散というものが何を意味しているか、どうして必要かというのを整理する必要があります。
ある母集団の性質を知りたいとき、母集団の中に含まれる個々のデータである標本について調べていくことで、母集団の持つ特徴を推定しようというのが統計調査であり統計学の目的です。
例えばそれらの標本に基づいて平均値や最頻値、中央値といった代表値を算出します。これによって、中心部分の傾向がおおよそわかるようになります。次に、母集団の外側の傾向にも注目し、その散らばり具合についても調べる必要があります。その散らばり具合を調べる手段の一つが分散(又は偏差)ということになります。
このとき、母集団に属する標本の数が調査できる程度の数しかない場合は、すべての標本について調査してしまえばよく、母集団の平均や母集団の分散といった傾向を直接把握できます。これを全数調査と呼びます。
しかし、調査対象が非常に膨大な標本から成る母集団であるときは、そのうち一部の標本のみを抽出して調査し、推定しなければなりません。これを標本調査と呼びます。
標本調査には標本誤差も含まれますが、様々な事情で全数調査が不可能である場合には、標本調査を用いて母集団の性質を推定します。
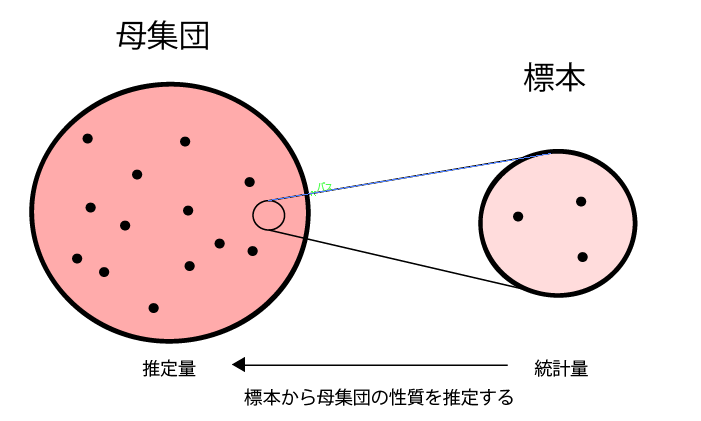
このとき、ランダムにn個抽出した標本の平均値(標本平均)の期待値は、母集団の標本の平均と一致するはずなのですが、ランダムにn個抽出した標本の分散(標本分散)については、どうやら母集団の分散よりも少しだけ小さくなってしまうのです。
それでは母集団の性質を推定するのに不都合が生じるので、その小さくなった分を補正したものが不偏分散です。
標本確率変数
母集団が有限個の、例えば3個の標本から成る場合、2個の標本を用いて得られる標本平均や標本分散は母集団平均や母集団分散と一致しないことは感覚的にもわかりますよね。
ここで確認しておかなければならないのは、標本の値そのものを母集団の平均や分散そのものと一致させようとしているわけではないし、それは無理ということです。ある標本を適当に抽出しようとするとき、その期待値が母集団の平均と一致しているかを確認しなければならないのです。
くどいくらいの説明になって申し訳ありませんが、離散的な値を取る事象の場合、一旦その事象を確率変数として考え、即ち標本平均の期待値や標本分散の期待値が母集団の平均や母集団の分散と一致していれば、母集団の性質がわかるわけです。
ということで、期待値を考えるために標本の抽出の際に、母集団の中の値を得る標本$x_{i}(i=1,2,3,\cdots,n)$というのは、標本確率変数$x_{i}$であり母集団と同じ確率分布に従うものであると考えることにしました。
標本平均$\bar{x}$の中の標本$x_{i}$と母集団から任意に抽出した標本$x_{i}$は当然ながら全く同じものです。
こうすることで、期待値を元に母集団に従う確率変数であるということが言えるようになります。この考えを元に一つずつ考えていきましょう。
平均値(代表値)とは
例えば平均値は、母集団に含まれる標本 $x_{i}$ (iは標本の数であり自然数 1,2,3,・・・)としたとき、$$平均値 \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i} = \frac{1}{n} ( x_{1}+x_{2}+\ldots+x_{n})$$と表現できます。
しかし、代表値(ここでは平均値)だけではこれらのデータがどの程度の散らばりを持っているのかを判別することができません。
そこで、この標本の散らばり具合を調べる方法が必要になります。
平均偏差とは
標本の散らばり具合を調べるにあたり、まずは標本の平均からそれぞれの標本がどのくらい値が離れているかについて調べてみることにしました。母集団から抽出した標本$x_{i}$について、平均値である$\bar{x}$との差(偏差)$x_{i}-\bar{x}$を考えます。
しかし、この$x_{i}-\bar{x}$の平均をとろうとすると、マイナス方向に散らばっている集団も存在するため必ずその相和は0になってしまいます。
$$x_{i}-\bar{x}の平均 \overline{$x_{i}-\bar{x}}=\frac{1}{n} \sum_{i=1}^{n}(x_{i}-\bar{x})$$
$$=\frac{1}{n} \sum_{i=1}^{n}x_{i}-\frac{1}{n} \sum_{i=1}^{n}\bar{x}$$
$$=\bar{x}-\frac{n}{n} \bar{x}$$
$$=\bar{x}-\bar{x}\\=0$$
そこで、それぞれの標本の持つ偏差について、絶対値をとり平均を求めることにしました。これは($平均偏差 MD$)と呼ばれます。
$$平均偏差MD=\frac{1}{n}\sum_{i=1}^{n}|x_{i}-\bar{x}|$$
標本分散とは
標本の散らばり具合を調べるのに平均偏差という手法を説明しましたが、実際にはあまり利用されていません。この点はそもそも誤差関数がどうとか様々な合理的理由があるので全てを説明するのは省略します。平均偏差自体は立派にばらつき具合を説明できていると思うのですが、平均偏差を最小にする代表値は中央値であり、平均を母集団の中心部分の特徴として説明した場合に当初の母集団の性質を説明するにもやや不都合があります。ほかに分散を加算できないなど数学的に使いにくい点などがあります。
そこで、もっと扱いやすい指標として平均値である$\bar{x}$との差(偏差)を自乗$(x_{i}-\bar{x})^{2}$して評価する手法が用意されました。(この何故自乗であるかという点も自分は引っかかってしまったことがあります。学生時代は自乗どころか4乗でもいいのではないかということでわざわざ4乗で計算したこともありました。しかし、各種計算をする上で結局遠回りをしているだけだったのでこの点については解説しません。興味のある人はやってみましょう。)
$$標本分散s^{2}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}$$
この平均偏差の弱点をカバーした標本分散の出現により、母集団の性質を説明することができるかのように思えました。
しかし、この標本分散には致命的な問題がありました。それは、標本群から作成した標本分散は、母集団が持つ母分散よりも少しだけ小さく計算されてしまうのです。
標本平均の期待値と母平均
標本確率変数$x_{i}$の期待値$E(x_{i})$は母平均$\mu$に等しく、標本確率変数$x_{i}$の分散$V(x_{i})$は母分散$\sigma^{2}$に等しくなります。また、母分散は期待値を用いて以下のように式変形できます。
$$E(x_{i})=E(x)=\mu$$
$$V(x_{i})=V(x)=\sigma^{2}$$
$$=E(x-\mu^{2})=E(x-E(x)^{2})$$
では、これを標本平均の期待値で考えてみます。
$$標本平均の期待値 E(x_{i})=E\frac{1}{n}\sum_{i=1}^{n}(x_{i})$$
$$=E\frac{1}{n}(x_{1}+x_{2}+\cdots+x_{n})$$
$$=\frac{1}{n}(E(x_{1})+E(x_{2})+\cdots+E(x_{n}))$$
$$=\frac{1}{n}(\mu+\mu+\cdots+\mu)$$
$$=\frac{n}{n}\mu=\mu$$
ということで標本平均の期待値は母平均と一致します。
このとき、標本確率変数$x_{i}$を母集団の不偏推定量であるといいます。
では標本平均の分散(ややこしい)は母分散とどのような関係にあるでしょうか。
$$標本平均の分散 V(\bar{x})=V(\frac{1}{n}\sum_{i=1}^{n}x_{i})$$
$$=\frac{1}{n^{2}}V\sum_{i=1}^{n}x_{i}$$
$$=\frac{1}{n^{2}}(V(x_{1})+V(x_{2})+\cdots+V(x_{n}))$$
$$=\frac{1}{n^{2}}(\sigma^{2}+\sigma^{2}+\cdots+\sigma^{2})$$
$$=\frac{n}{n^{2}}\sigma^{2}$$
$$=\frac{1}{n}\sigma^{2}$$
ということで、標本平均の分散は、標本数(サンプル数)を増やすほど、母分散よりも小さくなっていくことがわかります。n=1で標本確率変数$x_{i}$と一致しますから、その分散も当然母分散$\sigma^{2}$に等しくなります。これは、nが大きくなるほど、中心に近づきやすくなるという意味なのです。
賭博破戒録で学ぶ分散の基本
ところで、ここでしれっと
$$V(\frac{1}{n}\sum_{i=1}^{n}x_{i})=\frac{1}{n^{2}}V\sum_{i=1}^{n}x_{i}$$
という変形を用いています。
この変形を理解するには、分散の基本的な性質に着目する必要があります。
さいころの目を表す確率変数$Xai (=1~6)$があったとしましょう。このとき、分散$V(Xai)$は
$$V(Xai)=\frac{35}{12}$$
となります。
次に通常の3倍の値を表すさいころがある場合、確率変数$Xai3 (=3~18)$があったとしましょう。
$$V(Xai3)=\frac{315}{12}=V(Xai×3)=\frac{3^{2}×35}{12}=3^{2}×V(Xai)$$
と、分散は9倍に、 定数倍した確率変数の分散は、定数の自乗に比例することがわかります。
ちなみに、確率変数の分散については数式変換で使用するのでいくつか整理しておきましょう。例えば、賭博破戒録カイジのチンチロ編に出てきたピンゾロ賽は、確率変数$Xai1 (=1)$と定義することができます。この場合、$\bar{Xai1}=Xai=1$であることが明らかなので、
$$V(Xai1)=\frac{(1-1)^{2}}{6}+\frac{(1-1)^{2}}{6}+\frac{(1-1)^{2}}{6}+\frac{(1-1)^{2}}{6}+\frac{(1-1)^{2}}{6}+\frac{(1-1)^{2}}{6}=0$$
となり、分散0というのはブレなく確実に1の目が出るという意味です。
一方で456賽は
$$V(Xai456)=\frac{(4-5)^{2}}{6}+\frac{(4-5)^{2}}{6}+\frac{(5-5)^{2}}{6}+\frac{(5-5)^{2}}{6}+\frac{(6-5)^{2}}{6}+\frac{(6-5)^{2}}{6}$$
$$=\frac{(-1)^{2}}{6}+\frac{(-1)^{2}}{6}+\frac{(0)^{2}}{6}+\frac{(0)^{2}}{6}+\frac{(1)^{2}}{6}+\frac{(1)^{2}}{6}$$
$$=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}$$
$$=\frac{4}{6}=\frac{2}{3}$$
と、標本平均の期待値5を中心にややバラつきがあることがわかりますね。ちなみにこの456賽ですが、$Xai456=Xai123+3$というように定数加算の確率変数として定義することもできます。このとき、$V(Xai123)=\frac{2}{3}$となり、$V(Xai123+3)=V(Xai456)=V(\frac{2}{3})$となります。
つまり
$$V(x+c)==V(x)$$
が成立します。
結果に加算される定数が変化しても、 分散には影響しないのです。
賭博破戒録カイジの戦いは分散$V(Xai)=\frac{35}{12}$の通常プレイに対して、ハンチョウの456賽による分散$V(Xai)=\frac{2}{3}$という圧倒的有利に対して、分散$V(Xai)=0$という完全な作戦で勝ったということがわかりますね。
わかりやすい!さすが俺たちのカイジ先生・・・!(何が)
とまあ、細かなネタはともかく、以上の証明により以下の式
$$標本平均の分散 V(\bar{x})=\frac{1}{n}\sigma^{2}$$
というところだけしっかり押さえていただければ大丈夫です。この式が後々意味をもってくることになるのです。
標本分散の期待値と不偏分散
ここで、標本分散の期待値が母集団とどのような関係にあるかを調べなければなりません、ここで、標本分散を標本平均の式を用いて次のように変形します。
$$標本分散 s^{2}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}$$
$$=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu-\bar{x}+\mu)^{2}$$
$$=\frac{1}{n}\sum_{i=1}^{n}( (x_{i}-\mu)-(\bar{x}-\mu) )^{2}$$
$$=\frac{1}{n}\sum_{i=1}^{n}( (x_{i}-\mu)^{2}-2(x_{i}-\mu)(\bar{x}-\mu)-(\bar{x}-\mu) ^{2})$$
$$=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)^{2}-2\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)(\bar{x}-\mu)+\frac{1}{n}\sum_{i=1}^{n}(\bar{x}-\mu)^{2}$$
$$=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)^{2}-2\frac{n}{n}(\bar{x}-\mu)^{2}+\frac{n}{n}(\bar{x}-\mu)^{2}$$
$$=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)^{2}-(\bar{x}-\mu)^{2}$$
と、ここまで。
次に標本分散の期待値は
$$標本分散の期待値 E(s^{2})=E(\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2})$$
$$=E(\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)^{2}-(\bar{x}-\mu)^{2})$$
$$=\frac{1}{n}(\sum_{i=1}^{n}E(x_{i}-\mu)^{2}-nE(\bar{x}-\mu)^{2})$$
ここで、$E(x_{i})=E(\bar{x})=\mu$より
$$=\frac{1}{n}(\sum_{i=1}^{n}E(x_{i}-E(x_{i}) )^{2}-nE(\bar{x}-E(\bar{x}) )^{2})$$
このとき、$分散は偏差(確率変数と期待値との差 x-Ex)の自乗の期待値 V(x)=E(x-Ex)^{2}$であることから、
$$=\frac{1}{n}(\sum_{i=1}^{n}V(x_{i})-nV(\bar{x}) )$$
ここで、$V(x_{i})=\sigma^{2}$、$V(\bar{x})=\frac{1}{n}\sigma^{2}$を用いて
$$=\frac{1}{n}(\sum_{i=1}^{n}\sigma^{2}-n\frac{1}{n}\sigma^{2} )$$
$$=\frac{1}{n}n\sigma^{2}-\sigma^{2}$$
$$=\frac{1}{n}\sigma^{2}-\frac{1}{n}\sigma^{2}$$
$$=\frac{n-1}{n}\sigma^{2}$$
となります。式変形が長かったので再掲すると、
$$標本分散の期待値 E(s^{2})=\frac{n-1}{n}\sigma^{2}$$
これは右辺と左辺を変形すると
$$母分散 \sigma^{2}=\frac{n}{n-1}E(s^{2})$$
という形になり、標本分散の期待値に$\frac{n}{n-1}$を乗じると母分散になることを意味しており、これが不偏分散(の期待値)ということだ。
即ち、不偏分散は母分散の不偏推定量であるということなのである。
何故学校では教えなかったのか
当初は何故学校では不偏分散のn-1で除すことの証明を行わないのか、という疑問が生じたものの、実際に証明してみるとあっさりわかる。
物凄い労力なのである。
単にサンプルサイズnがn-1になるだけなのだが、確率変数、標本、分散、それぞれをきちんと理解していなければ辿り着けず、これから推測統計を始めるにあたり数学的な分野で躓かれては話にならないのだ。
高校の授業の限られたカリキュラムの中で、この証明だけで数時間を費やすのは得策でないのだろう。身近なサイコロを使って離散的確率統計の話に入った方がスムーズだし理解も早い。わかる。自分もサイコロを使って説明したし。
自分で書いていても本当に大変だった。そして次はやらないだろう・・・。
それでもこの記事を読んでくれた人にはお礼を言いたい。自分なりに詳しく書いたつもりだからね・・・
より良い方法、意見がありましたら、教えてくださいね。
※はてなblogのシグマ表記に問題があったため、ちょい修正しました。